Morgemil Part 8 – BSP Dungeon Generation Part 1

Towards my goal of interesting dungeon generation. I started looking into various techniques and the first thing to catch my eye was a visual explanation of BSP Dungeon Generation.

This appeals to me so I wrote out some code to do just that:

namespace Morgemil.Test
 
open Morgemil.Map
open Morgemil.Math
 
module BspGenerator =
  ///The smallest room possible
  let MinRoomSize = Vector2i(23, 23)
 
  ///Average more towards this size in theory
  let TargetRoomSize = Vector2i(41, 41)
 
  type Tree =
    | Node of Tree * Tree
    | Leaf of Rectangle
 
  type Axis =
    | Horizontal
    | Vertical
 
  ///Choose the opisite Axis
  let Opposite(ax : Axis) =
    match ax with
    | Axis.Vertical -> Axis.Horizontal
    | Axis.Horizontal -> Axis.Vertical
 
  let CanDivideHorizontal(area : Rectangle) = area.Width > MinRoomSize.X * 2
  let CanDivideVertical(area : Rectangle) = area.Height > MinRoomSize.Y * 2
  let CanDivide(area : Rectangle) = CanDivideHorizontal area || CanDivideVertical area
 
  ///Chooses an axis to split on. Keeps ratios fairly square.
  let AxisToDivide (ax : Axis) (area : Rectangle) =
    match area with
    | _ when area.Height >= area.Width * 2 -> Axis.Vertical
    | _ when area.Width >= area.Height * 2 -> Axis.Horizontal
    | _ when not (CanDivideHorizontal area) -> Axis.Vertical
    | _ when not (CanDivideVertical area) -> Axis.Horizontal
    | _ -> Opposite(ax)
 
  ///Rectangle * Rectangle
  let Divide (area : Rectangle) (ax : Axis) (rng : RNG.DefaultRNG) =
    match ax with
    | Axis.Horizontal ->
      let rng_width = RNG.Range rng (MinRoomSize.X) (area.Width - MinRoomSize.X)
      let first = Rectangle(area.Position, Vector2i(rng_width, area.Height))
      let second =
        Rectangle(area.Position + Vector2i(rng_width, 0), area.Size - Vector2i(rng_width, 0))
      (first, second)
    | Axis.Vertical ->
      let rng_height = RNG.Range rng (MinRoomSize.Y) (area.Height - MinRoomSize.Y)
      let first = Rectangle(area.Position, Vector2i(area.Width, rng_height))
      let second =
        Rectangle(area.Position + Vector2i(0, rng_height), area.Size - Vector2i(0, rng_height))
      (first, second)
 
  ///Recursively divides an area into a Binary Space Partitioning Tree
  let rec BSP (rng : RNG.DefaultRNG) (area : Rectangle) (ax : Axis) =
    let prob =
      (decimal ((area.Size - MinRoomSize).Area) / decimal ((TargetRoomSize - MinRoomSize).Area))
    let divide = CanDivide(area) && RNG.Probability rng prob
    match divide with
    | false -> Tree.Leaf area
    | true ->
      let opAx = AxisToDivide ax area
      let (first, second) = Divide area opAx rng
      Tree.Node(BSP rng first opAx, BSP rng second opAx)
 
  //This is essentially a constant since it takes no arguments
  let DungeonGenerator =
    let dungeonFloor =
      TileDefinition(1, "Floor", "Dungeon floors are often trapped", false, true, TileType.Land)
 
    let BspResults =
      ///Inject the seed in the future
      let seed = System.Random().Next()
      BSP (RNG.SeedRNG(seed)) (Rectangle(Vector2i(0, 0), Vector2i(234, 124))) Axis.Horizontal
 
    ///flatterns a BSPTree into Rectangle List
    let rec flatten treeNode =
      match treeNode with
      | Tree.Leaf(rect) -> [ rect ]
      | Tree.Node(e1, e2) ->
        [ flatten e1
          flatten e2 ]
        |> List.concat
 
    ///(0,0) (90,0) (180,0)...
    let chunksToCreatePositions = flatten BspResults
 
    ///Given the area of the chunk to create
    let CreateRoomChunk(roomArea : Rectangle) =
      ///border is empty tiles and the contained area is dungeon floor
      let ChooseTile(tilePosition : Vector2i) =
        match tilePosition with
        | _ when tilePosition.X = roomArea.Left || tilePosition.X = roomArea.Right
                 || tilePosition.Y = roomArea.Top || tilePosition.Y = roomArea.Bottom ->
          TileDefinition.Default
        | _ -> dungeonFloor
 
      ///Maps each coordinate in the room into a tile
      let tileArray =
        roomArea.Coordinates
        |> Seq.map (ChooseTile)
        |> Seq.toArray
 
      Chunk(roomArea, tileArray)
 
    chunksToCreatePositions |> Seq.map (CreateRoomChunk)

Here is the entry point

[<EntryPoint>]
let main argv =
  let createdBspDungeon = Morgemil.Test.BspGenerator.DungeonGenerator
  let filename2 = "map_test2.bmp"
  let dungeonDraw2 = Morgemil.Test.DungeonVisualizer.Visualize(createdBspDungeon)
  dungeonDraw2.Save(filename2)
  //System.Console.ReadKey() |> ignore
  0 // return an integer exit code

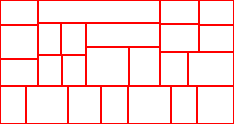
I made a quick visualizer to make a bitmap of the generated chunks

namespace Morgemil.Test
 
open System.Drawing
 
module DungeonVisualizer =
  open Morgemil.Map
  open Morgemil.Math
 
  ///Draws chunks to the minimum image space necessary
  let Visualize(chunks : seq<Chunk>) =
    let minimumImageSize =
      chunks
      |> Seq.map (fun chun -> chun.Area)
      |> Seq.reduce (+)
 
    ///Not a true FP structure. So modify at will.
    let resultingImage = new Bitmap(minimumImageSize.Width, minimumImageSize.Height)
 
    let DrawTile(tile : TileDefinition, pos : Vector2i) =
      let tileColor =
        match tile with
        | _ when TileDefinition.IsDefault tile -> Color.Red
        | _ -> Color.White
      resultingImage.SetPixel(pos.X, pos.Y, tileColor)
 
    let DrawChunk(chunk : Chunk) =
      chunk.Area.Coordinates
      |> Seq.map (fun xy -> (chunk.Tile xy, xy - minimumImageSize.MinCoord))
      |> Seq.iter (DrawTile)
 
    chunks |> Seq.iter (DrawChunk)
    resultingImage

Here is a sample result with the relevant parameters set:

  ///The smallest room possible
  let MinRoomSize = Vector2i(23, 23)
 
  ///Average more towards this size in theory
  let TargetRoomSize = Vector2i(80, 80)
 
  let seed = 67
  BSP (RNG.SeedRNG(seed)) (Rectangle(Vector2i(0, 0), Vector2i(560, 425))) Axis.Horizontal

What this does is define distinct areas in which to place distinct things without overlap. Those could be unique rooms, enough space for a specific kind of room generator, or just a way to determine room density. My next post on this subject will be on placing and connecting rooms.